Dear Editor: I wish to submit a research article (Short Communication) for publication in Nature, titled: “The formation of the four-way symmetric translational tiles (crystal) and corresponding unit cells.”
I believe that the study will significantly contribute to the body of literature as it tends to demonstrate how to construct a four-way symmetric Penrose tile. The results show that four-way symmetric Penrose tiling can be created by adding one more mirror coupling in the y-direction.
Further, given the widespread acceptance of five-fold rotational symmetry as a distinguishing feature of Penrose tiles, I believe that this paper will be of interest to the readership of your journal as it will pave the way for further investigations into four-way symmetric Penrose tiling. Study on the formation of four-way symmetric translational tiles is yet to be reported.
This manuscript has not been partially or fully published or presented elsewhere, and it is not being considered by another journal. I have read and understood your journal’s policies, and we believe that neither the manuscript nor the study violates any of these. There are no conflicts of interest to declare.
The formation of the four-way symmetric translational tiles (crystal) and corresponding unit cells
Key words: decagon, Penrose tiling, circular shape, translational periodic Penrose tiles, unit cell
Quoted from Wiki Penrose tiling (Here, a tiling is a covering of the plane by non-overlapping polygons or other shapes, and a tiling is aperiodic if it does not contain arbitrarily large periodic regions or patches. However, despite their lack of translational symmetry, Penrose tilings may have both reflection symmetry and fivefold rotational symmetry.) .
It is well known that Penrose tiles have a fundamental characteristic of aperiodicity.
A Penrose collage may have both reflection symmetry and fivefold rotational symmetry, but lack translational symmetry.. With such a well-known (and empowered) declaration of five-fold rotational symmetry, as a recognized characteristic of Penrose tiles, it seems that no one would believe that four-fold symmetric Penrose tiles are possible. As far as I know, no researchers have even attempted to draw four-way symmetric Penrose tiles. (It should be noted here that four-wat symmetry is actually not four-fold symmetry that the tile returns to its original shape after being rotated 90 degrees.)), here it just means that starting from the center point, in all four directions, the behavior of the tile is the same, it is up and down reflect symmetrical , as well as left to right symmetrical which is just a basic definition of mirror symmetry. In this post (short paper), we are just trying to show a way to draw a four-way symmetric Penrose tile..
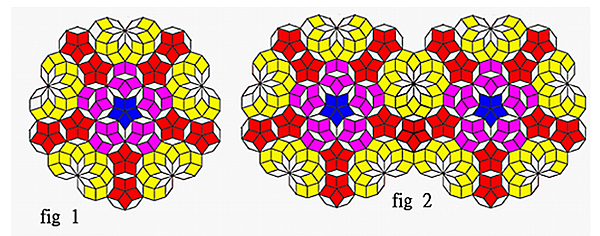
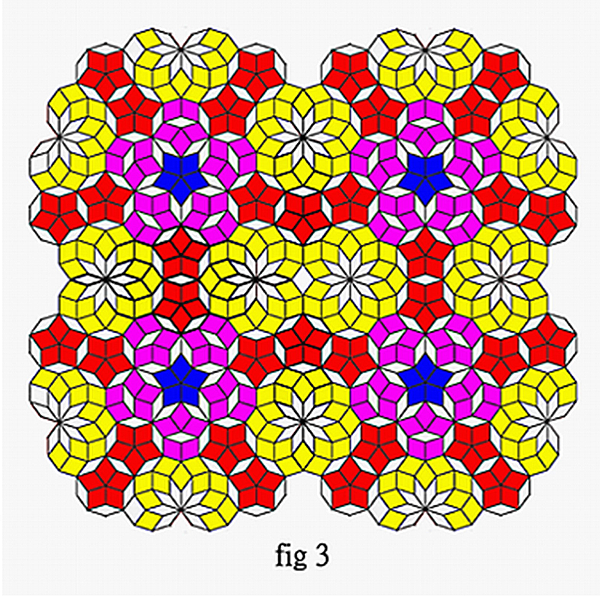
From my previous experience drawing different types of Penrose tiles, it was observed that it is possible to make four-way symmetrical Penrose tiles, as described below.. We can start with a Penrose tile as shown in Figure 1, which is a circular Penrose tile composed of four decagons of type -a, -b, -d, and -e. Using mirror coupling applied along the x-direction on the tiles in Figure 1, a mirror-symmetrical tile as shown in Figure 2 is produced, and then a mirror coupling is applied to the tiles in Figure 2 in the y-direction, the result is shown in Figure 3, This was followed by translational coupling using the tiles in Figure 3, resulting in a large Penrose tile as shown in Figure 4. One might notice that the rhombus marked dark gray in Figure 4 does not belong to any decagon。Here, the author uses the strict regulation (definition) to treat it as a defect。However, it is still a standard traditionally typical zero defect Penrose tiles.
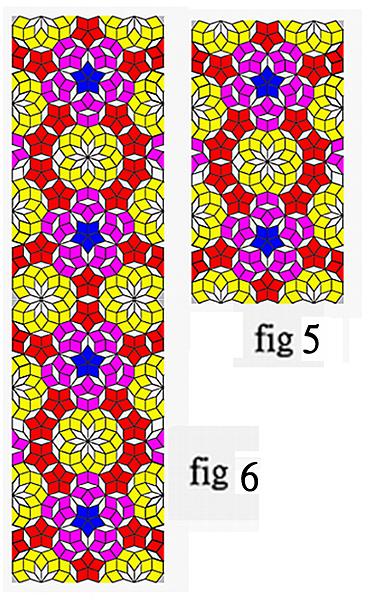
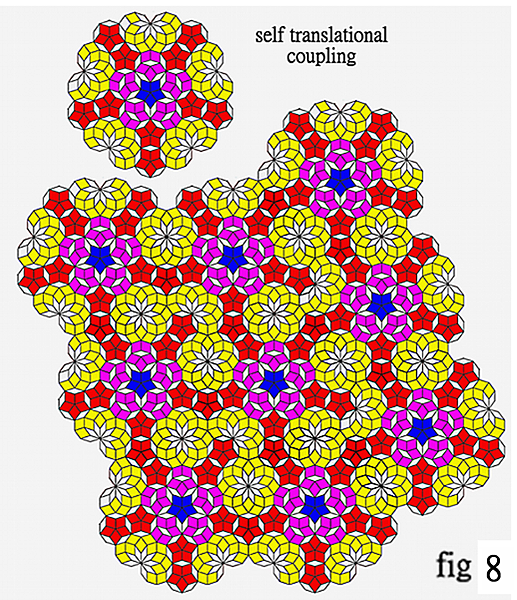
A basic unit can be easily extracted from Figure 5,carefully examine the tile in fig 5, and find it is not a real up side down symmetry. Appling one more mirror coupling in y-direction, a Four-way symmetric Penrose tiling, as shown in Figure 6 is produced.. After careful examination, this unit cell is symmetric on four directions. The tessellation of this unit cell reveals a four-way symmetric translational Penrose tiling, as shown in Figure 7. The most interesting finding is that, this Penrose tile in Fig. 1 can be self-extended translational by itself- coupling to infinity, as shown in the Fig. 8 . Unfortunately, the tile in fig 8 can go to infinity with a perceive structure at infinity while it is not five-fold symmetry nor a mirror symmetry. Therefore, It cannot be called a Penrose tile by conventional definition.






 留言列表
留言列表


