2023
I wish to submit a research article for publication in Nature, titled: “The formation of the periodic translational Penrose tiles (crystal) and their corresponding unit cells.”
I believe that the study significantly add to the body of literature because it aims describe the formation of binary circular Penrose tiles of translation mirror symmetry using a variety of permutations and combinations of coupling skills. The study shows that a penrose tube is made by rolling- up tiles in four directions, and a smallest Penrose football shape can be made using unit cell.
Further, I believe that this paper will be of interest to the readership of your journal because the establishment of a model of Penrose multiple concentric nanotube will pave the way for further investigations into 3-D Penrose-tiling. Study on formation of the periodic translational Penrose tiles is yet to be reported.
This manuscript has not been partially or fully published or presented elsewhere, and it is not being considered by another journal. I have read and understood your journal’s policies, and we believe that neither the manuscript nor the study violates any of these. There are no conflicts of interest to declare.
Thank you for your consideration. I look forward to hearing from you.
The formation of the periodic translational Penrose tiles (crystal) and their corresponding unit cells
ABSTRACT
Utilizing a variety of permutations and combinations of coupling skills, binary circular Penrose tiles of translation mirror symmetry have been constructed and their corresponding unit cells have also been defined. A tessellation of unit cells can perceive translational mirror Penrose tiles of infinite size and the number of such unit cells is infinite. A penrose tube is made by rolling- up tiles in four directions, and a smallest Penrose football shape can be made using unit cell
Key words: Decagon, Penrose tiling, binary tiling system, circular shape, translational periodic Penrose tiles, unit cell.
INTRODUCTION
Six different decagons can be formed using two rhombuses with acute angles of 36 and 72 degrees (Figure 1a), as shown in Figure 1b. Here, the fat rhombics of type-a, type-d, type-e, and type-f should be colored red, pink, yellow, and green blue, respectively, to facilitate the alignment and correction for the ensuing drawing of large Penrose tiles. These two rhombics were used by Penrose (Penrose, 1974) in 1974, which is over fifty years ago, to produce the famous Penrose-tile, which can be extended indefinitely (Figure 2). It is commonly known that Penrose tiles can exhibit both five-fold rotational symmetry and reflection symmetry, but not translational symmetry (Penrose, 1974). A circular shape Penrose-tile is created by edge cutting off of the original Penrose-tiling pattern as shown in Figure 3, which is a (so defined) binary Penrose-tiling system consisting of type-a and type-b decagons (shown in the Figure 1b). In this study, the translational symmetry of Penrose tiles is generated using circular Penrose tiles with reflection symmetry and five-fold rotational symmetry. This demonstrates the possibility of an infinite number of translational periodical Penrose tiles in the following: The fat rhombus in Type-a is highlighted in red in this circular Penrose tile. The other five-pointed stars are marked in green, with the exception of the one in the circular tile's center, which is marked in dark blue. It is intended to mention here that after the coupling process, new decagons and defects may be ingenerated, and tiles may not easily keep their original binary system. Therefore, author intended to keep “these non binary elements”.
Mirror symmetrical coupling in the X-direction yields the result shown in Figure 4a when the middle line of the leftmost type-a is used as a reference. The graphics obtained via mirror image coupling are presented in Figures 4b, 4c, and 4d for the second leftmost midline, third leftmost midline, fourth leftmost midline, and fifth leftmost midline, respectively, as the reference. It is important to note that after a mirror coupling, some other types of decagons can be seen in Figure 4 and are depicted by various colors. There are also some defects that are highlighted in gray. In this context, the term "defect" means that any additional rhombus or brick that does not belong to any of the above six regular decagons will be considered a defect, as will the absence of a rhombus in any decagon.
For the sake of simplicity, Figure 4d, which was retained as a binary system and defect-free graph, will be used as an example to illustrate how the coupling can continue in the y-direction for the sake of simplicity. Figure 5A shows after revision result of the specular deepest following the correction of the defect. It has been shown that complex, chaotic, and utterly undistinguishable patterns can be corrected (Steinhardt et al., 1998). Also, making the shallowest coupling in the same phase direction with the tiles in Figure 4e yields the result shown in Figure 6, which demonstrates that the boundaries of these two tiles are completely compatible (remain a binary system).
Due to their lack of five-fold symmetry while maintaining mirror symmetry, the revised tiles in the two examples above are no longer Penrose tiles according to the traditional definition of the term (Levine and Steinhardt, 1986; Socolar and Steinhardt, 1986). Nevertheless, they are all based on Penrose's original model and transformed through symmetrical coupling processing. They can be referred to as Penrose-like tiles.
Unit Cells of rectangular forms can be easily identified and extracted from Figures 5 and 6, as shown in Figure 5a and b, and utilizing these unit cells, it is possible to construct the translational Penrose -(like) tiles, as illustrated in Figures 5c and 6c. A defect-free translational periodic Penrose tile is shown in Figure 5c. As this elementary unit cell can be tessellated to construct a translational periodic Penrose tiling, the author intended to leave a variety of defects in Figure 6c to demonstrate that these defects will not prevent the formation of periodic tiles based on two distinct brick shapes (defect is meaningful only for the tiles built by decagonal tiling). Similar to rolling up various types of carbon nanotubes, four different Penrose tubes can be created by rolling up translating Penrose tiles in the x-direction or along the y-direction or along an 18-degree or 54-degree tilt angle. A three-dimensional Penrose unit in the shape of a football may be built by rolling on a unit cell.
Pseudo-three-dimensional Penrose tilings can be demonstrated by stacking several layers of translational Penrose tiling at a distance "a" from one another, and then each adjacent layer may create a 36 degree or a 72 degree slant shift. Penrose multilayer concentric nanotubes can provide important visualizations of how a potential bonding connection is established between two proximal layers and build a semi-3-D model to facilitate a further understanding of 3-D Penrose.
It may take a unit cell to make the Penrose tube, and with a dome-sealed tube, the smallest football-shaped three-dimensional Penrose football can be made, which could be very similar in structure to carbon C70… C80 and can be more translational; Penrose tiles contains more than 50% of TYPE-a star like structure (including the green color), which makes it simple to join tubes using carbon C 28, C60, C70…on dome region. The dome and tube seam regions may very well be made of distorted carbon grades C28, C60, or C70. One might envision that when tube size is large enough (that is, infinity), the dome may resemble a circular tile of infinite size (the center f tiles may be formed by five Decagon Type-e).
Summary
By edge-cutting the original five-fold rotated Penrose tile, the binary circular Penrose tile emerges. With the application of various combinations of coupling schemes, the existence of periodically translated Penrose tiles and their corresponding unit cells is demonstrated using only a single binary circular Penrose tile with different permutations and combinations. The infinitely large periodic translation Penrose collage can be perceived and realized by a tessellation of unit cells, and this unit cell can be recombined (tessellated, mosaiced) to form translational periodic Penrose tiles. Therefore, a model of Penrose multiple concentric nanotube is established to facility a further 3-D Penrose-tiling studies.

Figure 1. (a) Two rhombuses with acute angles of 36 and 72 degrees. (b) Six decagons, rhombics of type-a, type-d, type-e, and type-f are colored red, pink, yellow, and green blue, respectively,
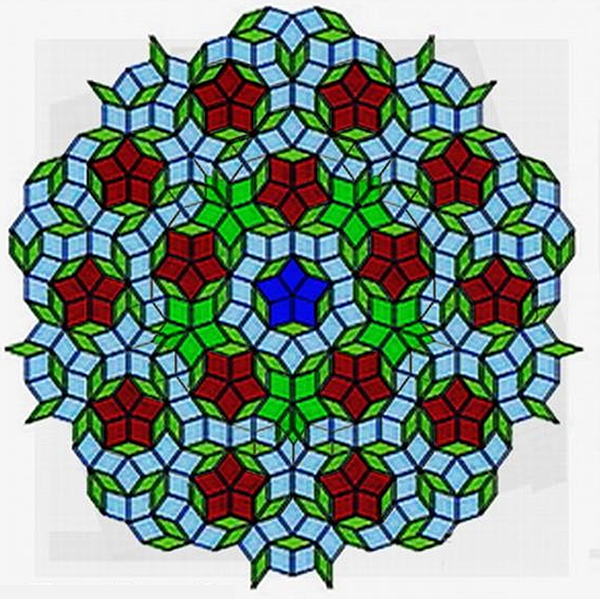
Figure 2. Penrose tile exhibits both five-fold rotational symmetry and reflection symmetry, but not translational symmetry (Penrose, 1974).
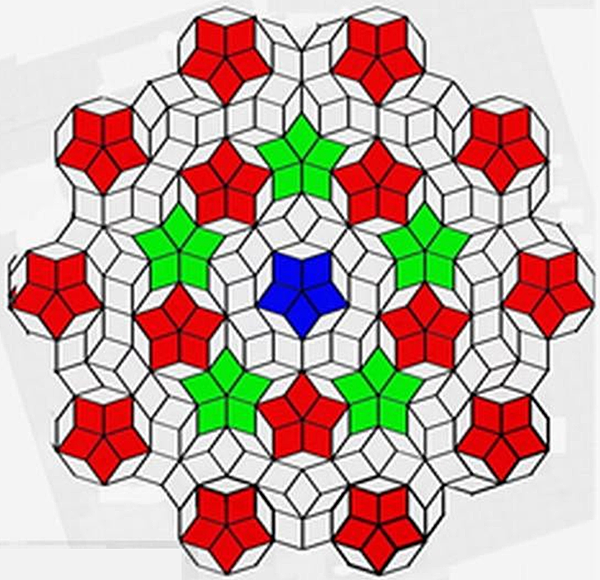
Figure 3. A circular shape Penrose-tile, consisting of type-a and type-b decagons. The fat rhombus in Type-a is highlighted in red, the other five-pointed stars are marked in green, the one in the circular tile's center, is marked in dark blue exceptionally.
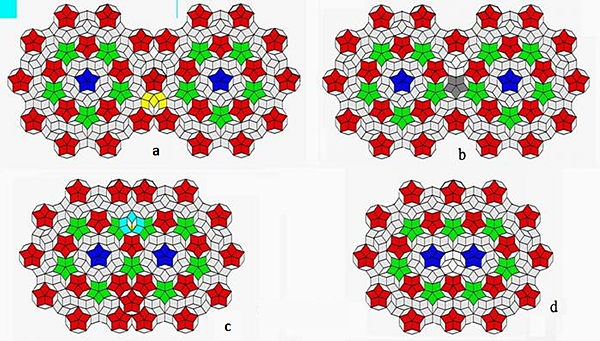
Figure 4. (a). Result of mirror symmetrical coupling for a circular tile in the X-direction when the middle line of the leftmost type-a is used as a reference. (b, c, and d) Mirror coupling for a circular tile in the X-direction, when the second leftmost midline, third leftmost midline, and fourth leftmost midline, respectively, as the reference. Some other types of decagons are depicted by various colors, and defects are highlighted in gray.
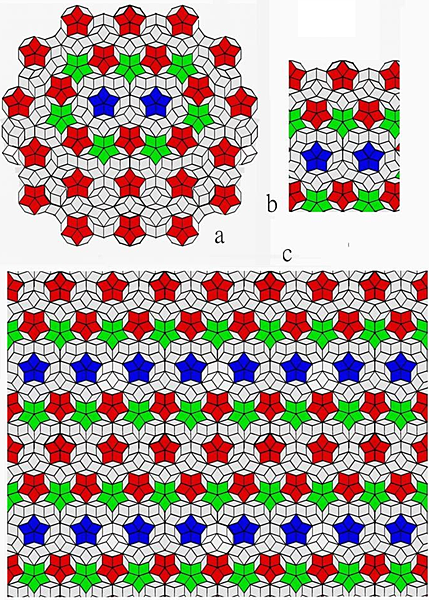
Figure 5. (a) A deepest specular coupling in the y-direction of the graphics in Figure 4d. (b) Graph of corresponding unit cell extracted from Figure 5a. (c) A defect-free translational binary tiling by tessellation of unit cell in Figure 5b.
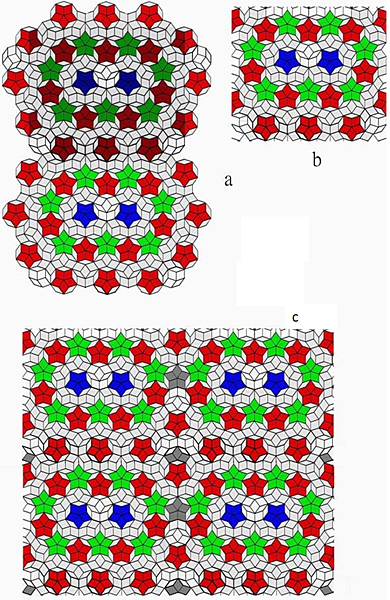

Figure 6. (a) Shallowest coupling in the same phase direction with the tiles in Figure 4d. (b) Graph of corresponding unit cell extracted from Figure 6a. (c) A translational binary tiling by tessellation of unit cell in Figure 6b, a variety of defects left.

Figure 7. Four different Penrose tubes can be created by rolling up translating Penrose tiles in the x-direction or along the y-direction or along an 18-degree or 54-degree tilt angle.
REFERENCES
Penrose R (1974). The role of aesthetics in pure and applird mathematical research. Bulletin of the Institute of Mathematics and Its Applications, 10:266-271.
Levine D, Steinhardt PJ (1986). Quasicrystals.I definition and structure. Phys. Rev. B 34: 617596 – Published 15 July 1986.
Socolar JES, Steinhardt PJ (1986). Quasicrystals. II. Unit-cell configurations. Phys. Rev. B 34:617 – Published 15 July 1986.
Steinhardt P, Jeong H-C, Tsai A (1998). Experimental verification of the quasi-unit-cell model of quasicrystal structure. Published 5 November 1998
5) Kun CY. Unpublished


 留言列表
留言列表


