or
I wish to submit a research article for publication in Communications Physics, titled: “Conjugated coupling for two Penrose tiles pair and their elementary unit cell for translation tiles.”
I believe that the study significantly add to the literature because it aims at creating two different types of pentagonal Penrose tiles in order to form translational periodic Penrose tiles. The results demonstrate that two Pentagonal-shaped Penrose tiles can be coupled successfully without any defect and at different depths.
Further, I believe that this paper will be of interest to the readership of your journal because the establishment of a model of Penrose multiple concentric nanotube will pave the way for further investigations into 3-D Penrose-tiling. Study on conjugated coupling for two Penrose tiles pair and their elementary unit cell for translation tiles has not been previously reported.
This manuscript has not been partially or fully published or presented elsewhere, and it is not being considered by another journal. I have read and understood your journal’s policies, and we believe that neither the manuscript nor the study violates any of these. There are no conflicts of interest to declare.
Conjugated coupling for two Penrose tiles pair and their elementary unit cell for translation tiles
ABSTRACT
The Penrose tiling, which is one of the most famous and complex tessellations, has been drawn and represented in many different ways, with most in artistic form. Consequently, two different types of pentagonal Penrose tiles are constructed in this study in order to create translational periodic Penrose tiles (crystals). It is found that these two Pentagonal-shaped Penrose tiles can be coupled successfully without any defect and at different depths. Therefore, a model of Penrose multiple concentric nanotube is established to facility a further 3-D Penrose-tiling studies.
Key words: Decagon, Penrose tiling, Pentagon shape, translational periodic Penrose tiles, unit cell.
INTRODUCTION
The Penrose tiling is one of the most well-known and complex tessellations. It has been drawn and depicted in numerous ways, with majority being in artistic form (Penrose, 1974). This five-fold symmetric Penrose tiling diagram helps to explain the five-fold nature of quasicrystals (Levine and Steinhardt, 1986) and as such inspired numerous studies in this field (Socolar and Steinhardt, 1986; Steinhardt et al., 1998). In the present study, the authors only focus on strictly defined error-free pentose tiling and how to extend tiling to infinity in a systematic and orderly manner. One of the systematic ways to draw defect-free Penrose tiles is to ensure that the tile is defect-free under strict definitions with a perceivable and repeatable internal structure that can be extended to infinity.
Six different decagons can be formed from two rhombuses with acute angles of 36 and 72 degrees (Figure 1). Using these two rhombuses, Penrose (1974) created the well-known Penrose-tile in 1974, which can be extended indefinitely, as shown in Figure 1. Following the original pattern configuration found by Penrose, several decagonal shapes were added outwards, resulting in a regular pentagonal pattern with five decagons on each side, as shown in Figure 2.The pattern consists of three decagons of types a, b, and c (or might be only type-a and type-b two decagons). The pentagon shape in Figure 2a appears a bit bloated. At the same time, a counterpart to a bulky Penrose tile was found, with a slightly slimmer pentagonal shape, as shown in Figure 2b.
All the vertices of each pentagonal Penrose tile are designated as a-type decagons (it is important to note that these five vertices can be substituted with other types of decagons, which may produce extensions in a variety of ways). To create the framework for future coupling alignment, type-a decagons in the dilated pentagonal tile (Figure 2a) are specially designated with red stars, while type-a decagons on the slim pentagonal tile (Figure 2b) are marked in green. The central regions of both bloated (dilated) and slim Pentagons are marked in dark blue for the purpose of coupling alignment.
Several examples of pair coupling are shown Figures 3, 4 and 5. Some of them still retain the mismatched regions to demonstrate the difficulty of producing defect-free Penrose tiles. The aforementioned various couplings may result in defects in the overlapping seam area. In most cases, these coupling defects can be easily removed to achieve even larger zero-defect Penrose tiles.
The examples of bottom-to-bottom opposite direction coupling in Figure 3, vertex-to-vertex opposing direction coupling in Figure 4, and bottom-vertex same direction coupling in Figure 5 illustrate in details these Bloated-slim types of coupling. Figure 3a shows a simple skin coupling; only the decades on outer layer are involved and perfectly coupled, necessitating no revision. Figure 3b shows a deeper coupling involving the outer three layers. Figure 3b1 shows the coupling before the revision, still retaining the remaining mismatched areas, while Figure 3b2 shows coupling after revision with the new type-e ingenerated (*created) to meet the defect-free requirements. Figure 3c shows an even deeper coupling covering almost all the region of the slim type tile (Figure 3c1) and is able to produce an incredible defect free revision (Figure 3c2). Figure 3d shows a completed coupling before and after the revision of these two pairs, while Figure 3d2 shows a circular Penrose tile. Figure 3e and f shows a slanted shift coupling of these Penrose tile pairs which also ingenerated a type-e decagon to meet the defect free requirement. Figure 4a shows the result of a deep coupling before revision, while Figure 4b and c shows the same coupling after revision.
Figure 5 shows the coupling results of the two Penrose tiles on the same direction. The Figure 5 demonstrates the bottom-vertex coupling type: 5(a1) before revision, 5(a2) after revision, (5b) a deeper coupling after revision, (5c) slant shift coupling after revision. The majority of defects in overlapped coupling can be fixed with some effort, as shown in Figures 3 and 4, but the process is not straightforward. The defects are left for readers to revise them and will not be discussed in this article. In fact, ignoring the defect ingenerated, all types of coupling can be performed easily for these two types of Penrose tiles, as shown in the case in Figure 5. These two Penrose tiles can be referred to as mutual conjugates since they have a high likelihood of coupling with one another under numerous distinct coupling conditions.
The different coupling mentioned above may result to defects in the overlapping seam area, and in most cases, these coupling defects can be easily removed to achieve a larger zero-defect Penrose tiles*( It should be noted that the traditional Penrose tiles allow the existence of defects)
All of these coupled pairs can themselves be translationally (or slanted shift) coupled as shown in Figure 6a and b to form translational aperiodic Penrose tiles. In this study, Figure 3c2 is utilized to illustrate self-coupled to infinity (as shown in Figure 7a) and from that point, the elementary unit cell is extracted (Figure 7b). Thus, this elementary unit cell can be tessellated to construct a translational periodic Penrose tiling.
Similar to rolling up different types of carbon nanotubes, four different Penrose tubes can be fabricated by rolling up a translating Penrose tiles along the x-direction, or along the y-direction, or along an 18-degree or 54-degree tilt angle. A three-dimensional Penrose unit ball may be constructed by performing rolling on a unit cell. These were all covered in another publication (Kun, Unpublished)
Summary
In this article, two distinct Pentagon-shaped Penrose tiles are constructed using the original Penrose tiling pattern. It is found that these two Pentagonal-shaped Penrose tiles can be coupled successfully without any defect and at different depths. An elementary unit cell can be extracted from repeated coupling results, and this unit cell can be recombined (tessellated, mosaiced) to form translational periodic Penrose tiles. Therefore, a model of Penrose multiple concentric nanotube is established to facility a further 3-D Penrose-tiling studies.

Figure 1. Original Penrose tile.

Figure 2. A regular pentagonal pattern with five decagonal on each side, (a) Bloated, (b) slim.
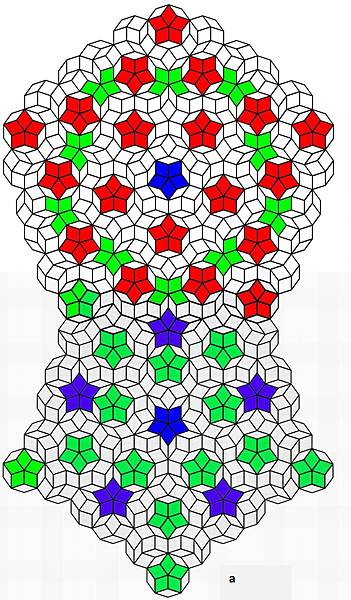
Figure 3a. The examples of bottom-to-bottom opposite direction coupling type; showing a simple skin perfectly coupling.
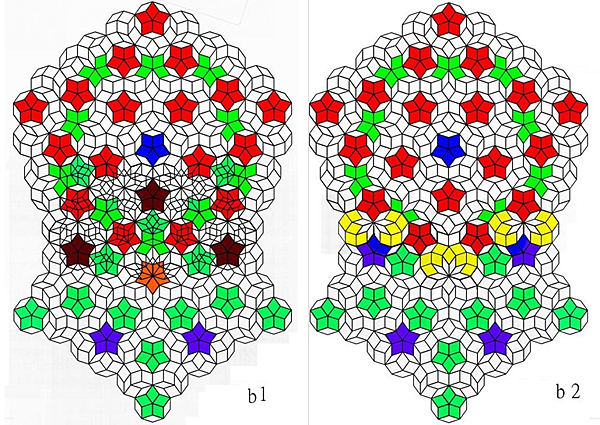
Figure 3b1 and b2. Deeper coupling, with outer three layers involved (3b1) coupling before revision remaining mismatched regions and (3b2) is after revision,
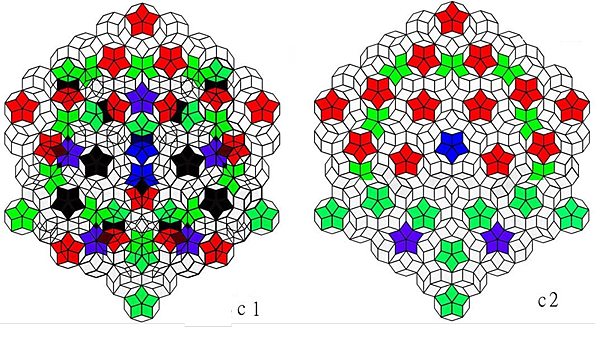
Figure 3c1 and c2. (3c) shows an even deeper coupling, covers almost all the region slim type tile, (3c1) before revision, (3c2) after revision
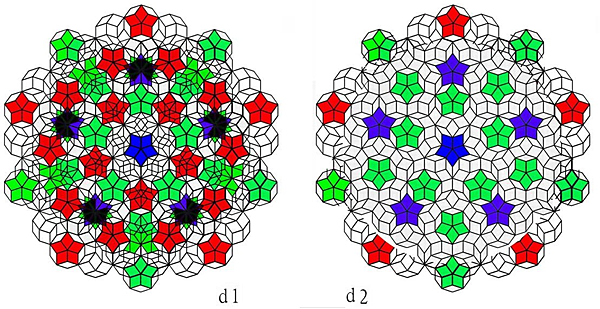
Figure 3d1 and d2. Completed coupling (3d1) before and (3d2) after revision revealed a circular Penrose tile.

Figure 3e. A slanted shift coupling.
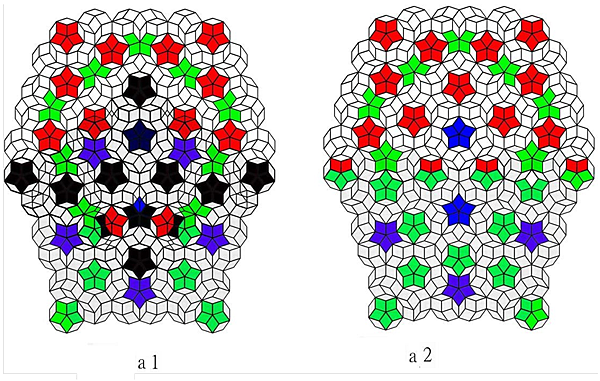
Figure 4. Examples vertex - to-vertex opposite direction coupling type, (4a) result of a deep coupling before revision, (4b) after revision.
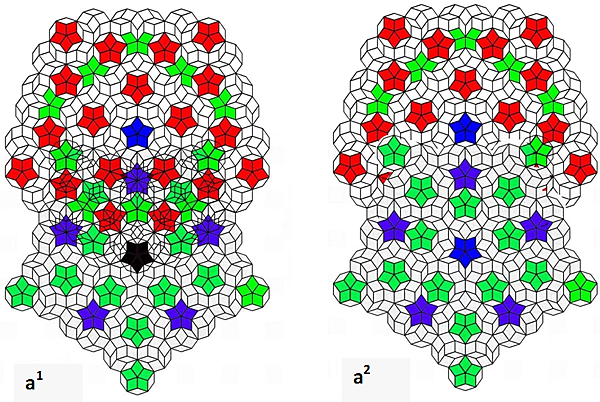
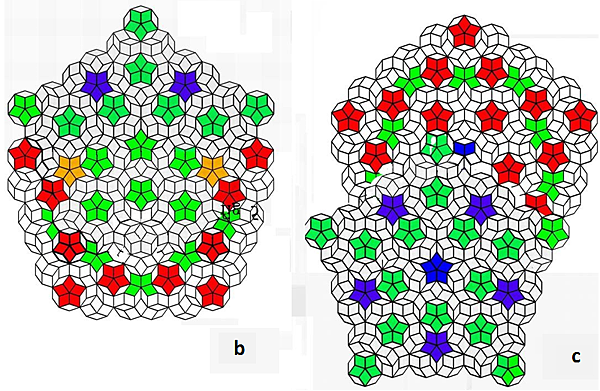
Figure 5. Bottom-vertex coupling in the same direction type: (a1) before revision, (a2) after revision, (5b) a deeper coupling after revision, (5c) slant shift coupling after revision.
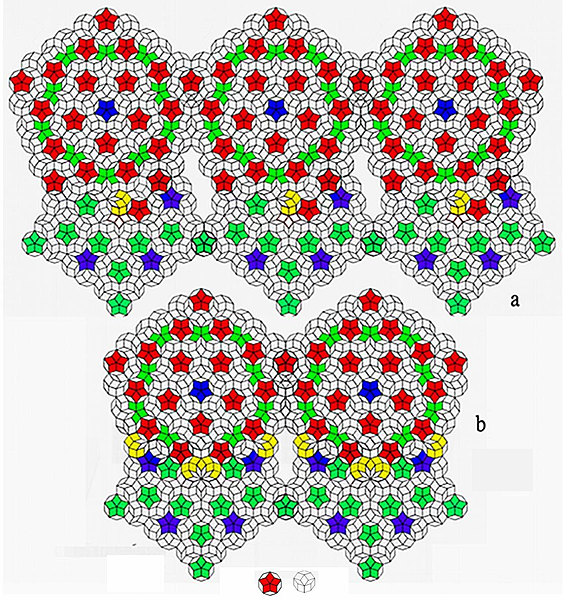
Figure 6. Coupled pairs can be translational (or slanted shift) coupled by their self.
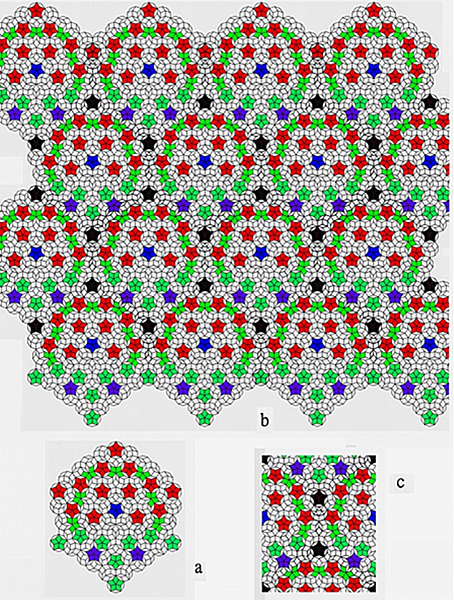
Figure 7. Tile in Figure (3c2) self-coupled to infinity, (b) a unit cell extracted from tile in Figure (a), and (c) unit cell can be tessellated to construct a translational periodic Penrose tiling.
REFERENCES
Penrose R (1974). The role of aesthetics in pure and applird mathematical research. Bulletin of the Institute of Mathematics and Its Applications, 10:266-271.
Levine D, Steinhardt PJ (1986). Quasicrystals.I definition and structure. Phys. Rev. B 34: 617596 – Published 15 July 1986.
Socolar JES, Steinhardt PJ (1986). Quasicrystals. II. Unit-cell configurations. Phys. Rev. B 34:617 – Published 15 July 1986.
Steinhardt P, Jeong H-C, Tsai A (1998). Experimental verification of the quasi-unit-cell model of quasicrystal structure. Published 5 November 1998
5 ) Kun CY. Unpublished


 留言列表
留言列表


