貢中元的部落格

The formation of the periodic translational Penrose tiles (crystal) and their corresponding unit cells 週期性平移彭羅斯瓷磚（晶體）及其相應晶胞的形成

A Penrose tiling is an example of an aperiodic tiling. Here, a tiling is a covering of the plane by non-overlapping polygons or other shapes, and aperiodic means that shifting any tiling with these shapes by any finite distance, without rotation, cannot produce the same tiling. However, despite their lack of translational symmetry, Penrose tilings may have both reflection symmetry and fivefold rotational symmetry. Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated them in the 1970s

從 Wiki 複製和google翻譯：

。彭羅斯平舖是非週期性平舖的一個例子。 在這裡，平舖是指由不重疊的多邊形或其他形狀覆蓋平面，非週期性意味著將具有這些形狀的任何平鋪移動任何有距離而不旋轉，不會產生相同的平鋪。 然而，儘管缺乏平移對稱性，彭羅斯拼貼可能同時具有反射對稱性和五重旋轉對稱性。Penrose tilings 以數學家和物理學家 Roger Penrose 的名字命名，他在 1970 年代對它們進行了研究

  Chung Yuan Kung , retired  Professor , Chung Hsing University, Taichung, Taiwan, ROC

.

    Key words: decagon, Penrose tiling, binary tiling system, circular shape, translational periodic Penrose tiles, unit cell

Abstract Binary circular Penrose tiles have been fabricated and using different permutations and combinations of coupling skills demonstrates the existence of periodically translation mirror symmetry Penrose tiles and their corresponding unit cells have been defined as well. A tessellation of unit cells can perceive translational mirror Penrose tiles of infinite size and the number of such unit cells is infinite.

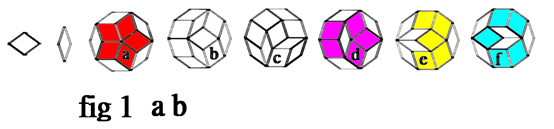
Two rhombic shapes with acute angle 36 and 72 degree can make six different decagons Fig 1. In 1974 almost fifty years ago Penrose (1) using these two rhombic created a famous Penrose-tile which can be extended unlimitedly, as shown in Fig 2a. It has been well known that Penrose tiling may have both reflection symmetry and fivefold rotational symmetry while lack of translational symmetry. (2) . In this paper, the translational symmetry of Penrose tiles is generated by using circular Penrose tiles with reflection symmetry and five-fold rotational symmetry, and demonstrates the possibility of an infinite number of translational mirror symmetric periodic Penrose tiles.

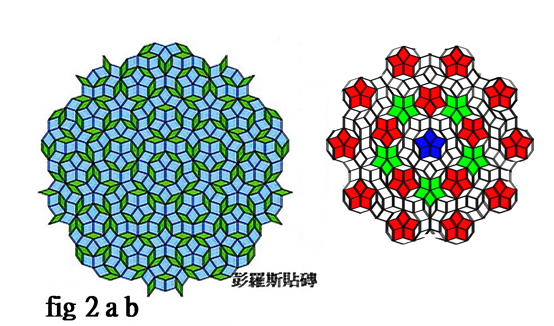
A circular shape Penrose-tile is created by edge cutting off of the original Penrose-tiling pattern as shown in Fig 2b, which is a (so defined) binary Penrose-tiling system consists of type-a and type-b decagons shown in the fig 1. In this paper, the translational symmetry of Penrose tiles is generated by using circular Penrose tiles (with reflection symmetry and five-fold rotational symmetry, which shows the possibility of an infinite number of translational periodical Penrose tiles in following.  

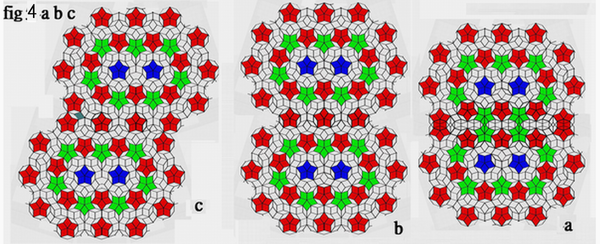
a proper reflect of the circular Penrose -tile coupling map is conducted on x- direction and result in following configurations as demonstrated in the fig 3 a ,b, c. Again, the coupling skill, mentioned above can be applied on the vertical Y-direction: Coupling defined here is different from tessellation. It refers to two graphics with the same or different internal structure configurations, which overlap to form a larger graphic by partial matching;  The misaligned area of the seam zone after coupling can be replaced or modified by any of the six decagons in Figure 1 without affecting nearby existing structures.  There are several coupling techniques that could be applied to extend this circular Penrose tiling to infinite are demonstrated. Here only take the pure binary configuration in the fig 3a, as an example to show a detail works of these basic techniques. Three schemes were suggested to try: (A) by up-side down (mirror reflected) depth coupling, as shown fig 4a,(B) by (vertical ) parallel skin coupling, as shown in fig 4b , and (C) by slanted shift coupling as shown in fig 4c . As well, the above configurations of that in fig 3 a, b, c, perform a coupling map on y-direction, result in the configurations as demonstrated in fig 4 a , b, c.

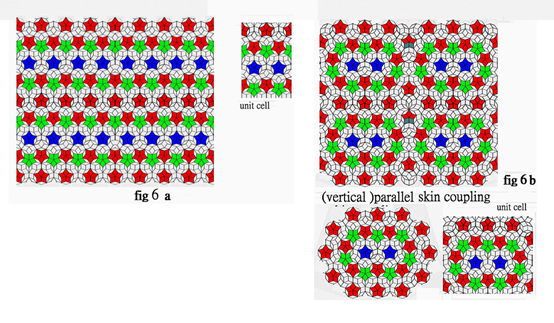
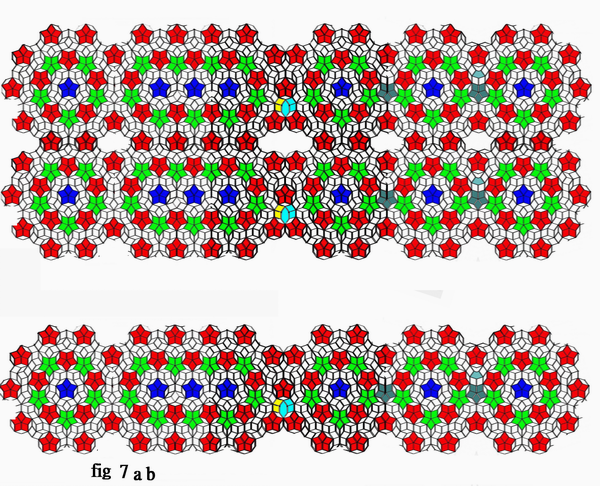
 A proper rectangular zone can always be located and cut off from the configurations in the fig. 4 . Those proper zone cut from the configurations the in the fig 4 a b , are demonstrated in fig 5 a b . These so called proper zones can be considered and be defined as unit cell corresponding to the configurations generated by different coupling schemes as mentioned above and are considered as a base build up to construct the translational Penrose tiles. Thus, the translational periodic Penrose tiles can be demonstrated by tessellation of each individual unit cell as demonstrated in fig 6 a b . The (non-five-fold) mirror symmetry translational periodic Penrose tile is therefore established. The circular Penrose tile can be coupled through different permutations and combinations of the above mentioned coupling schemes and generate unlimited various Panrose-tiling configurations, as demonstrated in fig 7 a b ,and unlimited unit cell can be cut off. The possibility of generating infinite units and infinite number of the translational Penrose tiles is perceptible and unerstandable. 

 is perceptible and understandable.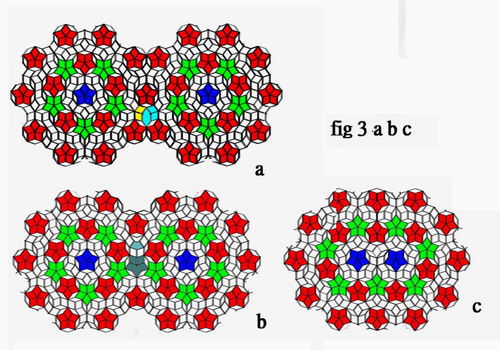

同樣，上述配置在 y 方向上執行耦合映射，導致如圖 4 a、b、c 所示的配置。總是可以定位並切掉合適的矩形區域，這些合適的區域從圖4的配置切出並在圖5中展示。這些所謂的適當區域被定義為單位單元，每個單位單元對應於如上所述的不同耦合方案生成的配置。這些所謂的適當區域可以被認為並定義為與如上所述的不同耦合方案生成的配置相對應的單位單元。並被視為構建平移彭羅斯瓷磚的基礎。因此，平移的彭羅斯拼塊可以通過每個單獨的晶胞的鑲嵌來證明，如圖 6 a b c 所示。因此建立了非五重對稱平移彭羅斯瓷磚。通過上述耦合方案的不同排列組合，可以產生無限個單元。通過上述耦合方案的不同排列組合，生成無限單元和無限平移的Penrose tiles的可能性是可感知和理解的。